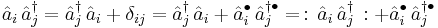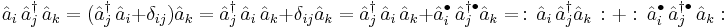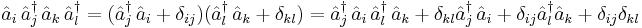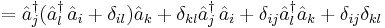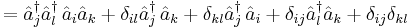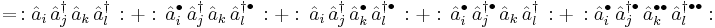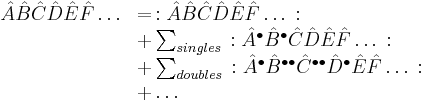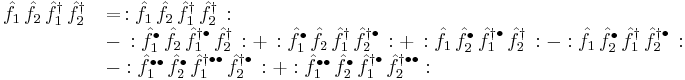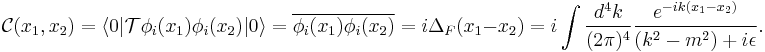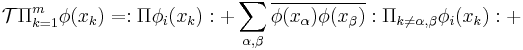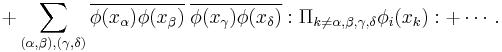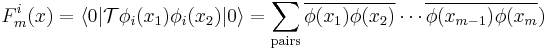Wick's theorem
| Quantum field theory |
|---|
| History of... |
|
Incomplete theories
|
|
Scientists
Adler • Bethe • Bogoliubov • Callan • Candlin • Coleman • DeWitt • Dirac • Dyson • Fermi • Feynman • Fierz • Fröhlich • Gell-Mann • Goldstone • Gross • 't Hooft • Jackiw • Klein • Landau • Lee • Lehmann • Majorana • Nambu • Parisi • Polyakov • Salam • Schwinger • Skyrme • Stueckelberg • Symanzik • Tomonaga • Veltman • Weinberg • Weisskopf • Wilson • Witten • Yang • Yukawa • Hoodbhoy • Zimmermann • Zinn-Justin
|
Wick's theorem is a method of reducing high-order derivatives to a combinatorics problem (Philips, 2001). It is named after Gian-Carlo Wick. It is used extensively in quantum field theory to reduce arbitrary products of creation and annihilation operators to sums of products of pairs of these operators. This allows for the use of Green's function methods, and consequently the use of Feynman diagrams in the field under study.
Contents |
Definition of contraction
For two operators  and
and  we define their contraction to be
we define their contraction to be
where  denotes the normal order of operator
denotes the normal order of operator 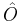
There is alternative notation for this as a line joining 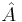 and
and 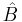 .
.
We shall look in detail at four special cases where 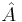 and
and 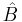 are equal to creation and annihilation operators. For
are equal to creation and annihilation operators. For  particles we'll denote the creation operators by
particles we'll denote the creation operators by 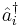 and the annihilation operators by
and the annihilation operators by 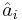 (
(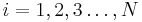 ).
).
We then have
where 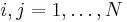 and
and 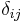 denotes the Kronecker delta.
denotes the Kronecker delta.
These relationships hold true for bosonic operators or fermionic operators because of the way normal ordering is defined.
Wick's theorem
We can use contractions and normal ordering to express any product of creation and annihilation operators as a sum of normal ordered terms. This is the basis of Wick's theorem. Before stating the theorem fully we shall look at some examples.
Examples
Suppose 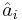 and
and 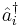 (
(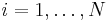 ) are bosonic operators satisfying the commutation relations:
) are bosonic operators satisfying the commutation relations:
where 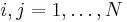 ,
, ![\left[ A, B \right]_- \equiv AB - BA](/2012-wikipedia_en_all_nopic_01_2012/I/086362d0cf83310d583e6b68f61dcf44.png) denotes the commutator and
denotes the commutator and 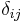 denotes the Kronecker delta.
denotes the Kronecker delta.
We can use these relations, and the above definition of contraction, to express products of 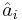 and
and 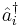 in other ways.
in other ways.
Example 1
Note that we have not changed 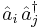 but merely re-expressed it in another form as
but merely re-expressed it in another form as 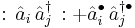
Example 2
Example 3
In the last line we have used different numbers of  symbols to denote different contractions. By repeatedly applying the commutation relations it takes a lot of work, as you can see, to express
symbols to denote different contractions. By repeatedly applying the commutation relations it takes a lot of work, as you can see, to express 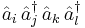 in the form of a sum of normally ordered products. It is an even lengthier calculation for more complicated products.
in the form of a sum of normally ordered products. It is an even lengthier calculation for more complicated products.
Luckily Wick's theorem provides a short cut.
Statement of the theorem
For a product of creation and annihilation operators 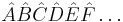 we can express it as
we can express it as
In words, this theorem states that a string of creation and annihilation operators can be rewritten as the normal ordered product of the string, plus the normal-ordered product after all single contractions among operator pairs, plus all double contractions, etc., plus all full contractions.
Applying the theorem to the above examples provides a much quicker method to arrive at the final expressions.
A warning: In terms on the right hand side containing multiple contractions care must be taken when the operators are fermionic. In this case an appropriate minus sign must be introduced according to the following rule: rearrange the operators (introducing minus signs whenever the order of two fermionic operators is swapped) to ensure the contracted terms are adjacent in the string. The contraction can then be applied (See Rule C'' in Wick's paper).
Example:
If we have two fermions (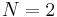 ) with creation and annihilation operators
) with creation and annihilation operators 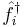 and
and 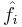 (
(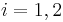 ) then
) then
Wick's theorem applied to fields
Which means that 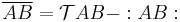
In the end, we arrive at Wick's theorem:
The T-product of a time-ordered free fields string can be expressed in the following manner:
Applying this theorem to S-matrix elements, we discover that normal-ordered terms acting on vacuum state give a null contribution to the sum. We conclude that m is even and only completely contracted terms remain.
where p is the number of interaction fields (or, equivalently, the number of interacting particles) and n is the development order (or the number of vertices of interaction). For example, if 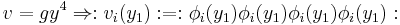
This is analogous to the corresponding theorem in statistics for the moments of a Gaussian distribution.
Note that this discussion is in terms of the usual definition of normal ordering which is appropriate for the vacuum expectation values of fields. There are any other possible definitions of normal ordering, and Wick's theorem is valid irrespective. However Wick's theorem only simplifies computations if the definition of normal ordering used is changed to match the type of expectation value wanted. That is we always want the expectation value of the normal ordered product to be zero. For instance in thermal field theory a different type of expectation value, a thermal trace over the density matrix, requires a different definition of normal ordering is needed (Evans and Steer, 1996).
See also
References
- G.C. Wick, The Evaluation of the Collision Matrix, Phys. Rev. 80, 268 - 272 (1950)
- S. S. Schweber, An Introduction to Relativistic Quantum Field Theory, Harper and Row, New York (1962). (Chapter 13, Sec c)
- M. E. Peskin and D. V. Schroeder, An Introduction to Quantum Field Theory, Perseus Books (1995). (§4.3)
- Tony Philips (11 2001). "Finite-dimensional Feynman Diagrams". What's New In Math. American Mathematical Society. http://www.math.sunysb.edu/~tony/whatsnew/column/feynman-1101/feynman1.html. Retrieved 2007-10-23.
- Emilio San Fabian (2 2001). "Wick's theorem". http://www.ua.es/cuantica/docencia/otros/cc/node15.html. Retrieved 2008-07-29.
- T.S. Evans, D.A. Steer, Wick's theorem at finite temperature, Nucl. Phys B 474, 481-496 (1996) arXiv:hep-ph/9601268
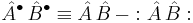
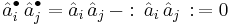
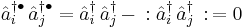
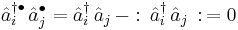
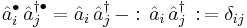
![\left [\hat{a}_i^\dagger, \hat{a}_j^\dagger \right]_- = 0](/2012-wikipedia_en_all_nopic_01_2012/I/a4f6629074a326065c92571d7c098397.png)
![\left [\hat{a}_i, \hat{a}_j \right]_- = 0](/2012-wikipedia_en_all_nopic_01_2012/I/a77cccca9ab6c06f79c07e07b19f636b.png)
![\left [\hat{a}_i, \hat{a}_j^\dagger \right ]_- = \delta_{ij}](/2012-wikipedia_en_all_nopic_01_2012/I/93094453c53ecbd17766c20f259abd22.png)